Fluids Simulation

COMSOL based fluid simulation of interactions between thermoelectric and soda can

Have you wonder how effective is thermoelectric in rejecting heat from an enclosed space? Currently, commericially available thermoelectric have an efficiency of approximately 5 to 6 percent. One of my favorite drink is Coca-Cola, and I occasionally wonders if there exists portable cooler where you could cool the soft drinks. In this project, I will provide a simulation of the cooling effect of thermoelectric device with COMSOL, numerical simulation with MATLab, and experimental data. For the COMSOL specifically, two configurations of cooling (vertical and horizontal can) are simulated to determine which method is better for cooling.

Computational Setup

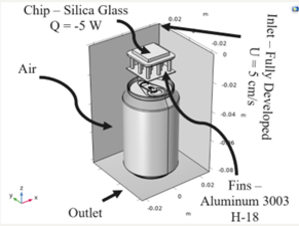
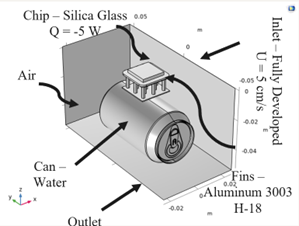
On the left, schematic of the verticle can. Right, schematic of the horizontal can.
On the left, the discretization of the verticle can's computational domain using tetrahedrals. Right, the discretization of the verticle can's computational domain using tetrahedrals.

The material properties of all the material included in the simulation is shown in the table below. Note that the air flow speed is assumed to be small which means that the flow condition will be laminar and not turbulent.

Material Material Density [kg/m3] Thermal Conductivity [W/m·K] Thermal Capacity [J/kg·K]
Air 1.208 0.02623 1006
Aluminum 2730 155 893
Water 997 0.598 4184
Silica Glass 2203 1.38 703

Theoretical Foundation

Before devling into the results of the simulation, let us discuss the governing equation of the interactions between the Coca-Cola can and the thermoelectric device. In addition, the Coca-Cola is assumed to be a solid with a material properties similar to that of water. Within the Coca-Cola can, the heat transfer is governed by the 3D heat equation:

\[C_p k \frac{\partial T}{\partial t} = \nabla^2\cdot T + q_k\]

Here, \(C_p\) represents heat capacity, k represents the thermal conductivity, T represents the temperature, (x, y, z) represents the spatial variable, and t represents the time variable. The behavior of the fluid within the closed system is governed by the Navier-Stokes equations ass shown in the equation below. The natural convection only occurs in the z-axis; therefore, the gravity term in the x-direction and y-direction of the Navier-Stokes equations are zeros.

\[\frac{\partial \vec{u}}{\partial t} + \vec{u} \left(\vec{u} \cdot \nabla \right)= -\nabla\vec{p} + \frac{\mu}{\rho}\nabla^2\vec{u} + \vec{g}\]

Here \(\mu\) represents the viscocity of fluid, p represents the pressure, u represents the velocity vector, and \(\rho\) represent the density of fluid. Since the fluid will carry the temperature as it flows from one location to another, the fluid motion and the corresponding temperature can be described with the temperature convection-diffusion equation.

\[\frac{\partial T}{\partial t} + \vec{u} \cdot \nabla T = \alpha (\nabla^2 T)\]

COMSOL Results

The surface temperature profile of the vertical and horizontal configuration of Coca-Cola Can.

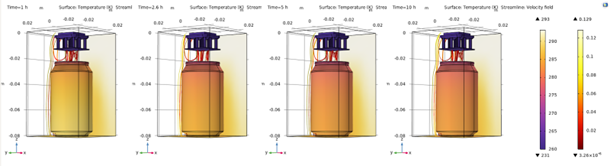
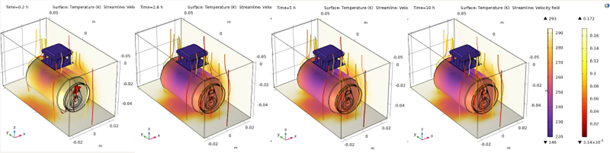
From the surface temperature graphs, the cooling effect of the horizontal configuration is 12.5% more effective than the standing configuration. For a much more symmetric cooling, the horizontal configuration should be utilized over the vertical configuration if using thermoelectric device as the main source of cooling.

On the left, slices of the velocity field around the Coca-Cola can in the vertical configuration. Right, slices of the velocity field around the Coca-Cola can in the configuration configuration.

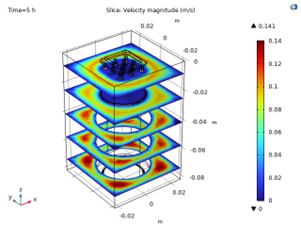
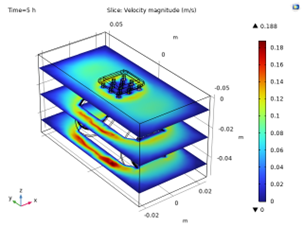
The maximum velocity for the standing and horizontal configurations are 0.141 m/s and 0.188 m/s, respectively. Notably, the maximum velocity in the horizontal setup exceeds that of the standing configuration by 33%. The greater maximum velocity in horizontal configuration likely contributes to the significantly enhanced heat transfer observed in the horizontal setup. However, it is evident that the velocity profile exhibits greater symmetry in the standing configuration without any significant effect on the heat transfer.

MATLab Numerical Studies

For the numerical study, the surface temperature on the Coca-Cola is obtained using the lumped capacitane model. It is assumed that the heat transfer coefficient, denoted by h, remains constant throughout the operation of the device.

\[T_s(t) = (T_i - T_{\inf})e^{\frac{hA_s}{\rho C_pV}t} + T_{\inf}\] \[q^{"}(t) = h(T_s(t) - T_{\inf})\]

Here \(T_s(t)\) represents the surface temperature, \(T_{\inf}\) represents the ambient temperature, h represent the heat transfer coefficient, and \(A_s\) represents the surface aera.

Numerical Results

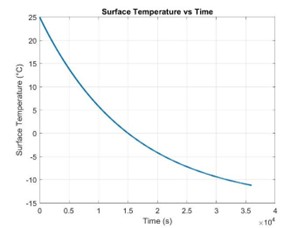
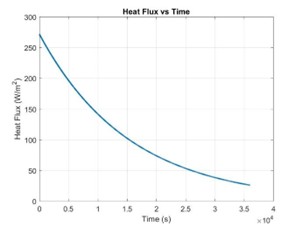
On the left, the surface temperature using the lumped capacitance model. Right, the heat transfer across the solid and fluid assuming constant heat source.
On the left, the axis-symmetric geometry of the Coca-Cola can. Right, the discretization of the geometry using triangular structures.
On the left, the temperature distribution at t=3hr. Middle, the temperature distribution at t=5hr. Right, the temperature distribution at t=10hr.

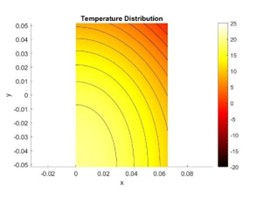
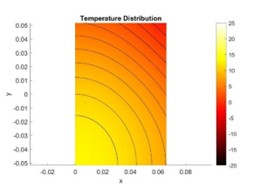
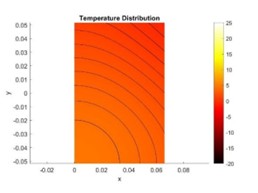
At the three-hour mark, the internal temperature of the Coca-Cola can remains 15 degrees Celsius. As the cooling time increases to the five-hour mark, majority of the can reachs a 10 degrees Celsius except for the bottom left corner. To fully reach the desired 5 degree Celsius, it will require 10 hours of cooling at a constant heat flux of -5W. For the experimental section of the fluid simulation, the thermoelectric device is enclosed in a “perfectly thermal isolated” environment where the cold side of device is expose to the air inside and the hot side facing the ambient environment.

Experimental Results

On the left, the exterior of the experimental setup. Right, the internal of the experimental setup with the thermal insulation.
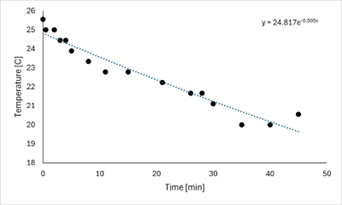
The experimental result over an hour of data recording.

Conclusion

This study investigated the efficiency of a closed-system cooling device utilizing the Seebeck effect of a thermoelectric device (TED) through COMSOL simulation, numerical modeling, and experimental analysis. The results revealed that the horizontal configuration of the cooling system outperforms the standing configuration, achieving a temperature approximately 12.5% lower, highlighting the importance of system orientation in TED-based cooling devices. Despite this, the study also identified the limitations of thermoelectric cooling for beverage applications, with prolonged cooling times and inefficiencies in heat extraction indicating a need for further optimization. While TED-based cooling shows promise, its performance currently lags behind conventional cooling methods, offering opportunities for future improvements and innovations in thermoelectric cooling technology.