3D Molecular Tagging Velocimetry

Introduction

Molecular Tagging Velocimetry (MTV) is a powerful flow measurement technique particularly well-suited for high-speed flows, where traditional methods like Particle Image Velocimetry (PIV) face significant limitations. Unlike PIV, which relies on seeding the flow with tracer particles, MTV directly tags nascent molecular species within the fluid. This eliminates the issue of inertial drag that causes tracer particles to lag behind flow at supersonic and hypersonic speeds. By capturing the displacement of tagged molecules over time, MTV can accurately measure velocity fields without introducing foreign particles, ensuring precision even in extreme flow conditions.

Governing Theory

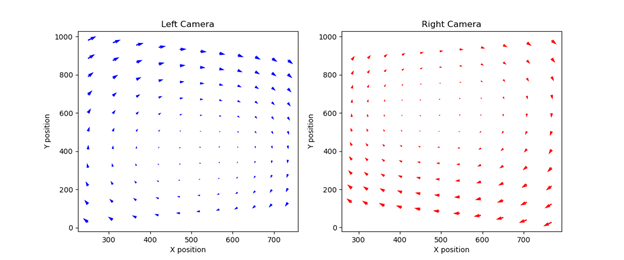
To extend MTV’s capability from two-dimensional to three-dimensional velocity measurements, a stereoscopic MTV (sMTV) setup is employed. This approach utilizes two cameras positioned at different angles to observe the same region of interest, enabling the capture of out-of-plane flow components that are otherwise unresolvable in 2D MTV. The stereoscopic setup introduces depth perception by analyzing the disparity between the two images, which is mapped from image to the object plane through polynomial based geometric calibration

To represent the polynomial calibration for the 3D reconstruction, the equation is expressed as:

\[\sum_{i=0, j=0, k=0}^{i=n, j=n, k=n} A_{i,j,k} \, x^i y^j z^k\]

Here, \(A_{i,j,k}\) represents the polynomial coefficients, while (x, y, z) denote the spatial coordinates in the object plane.

Calibration Process

On the left, images of the checkerboard taken from two different angularly positioned camera. On the right, the checkerboard board corners are detected to determine the image plane coordinate of the feature points.

On the left, schematic of the calibration process using Soloff polynomial [Pavlik et al.]. On the right, the schematic for 3D velocity field calculation using Soloff polynomial.

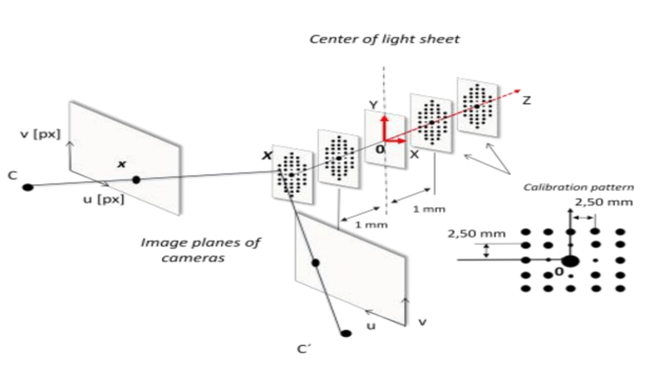
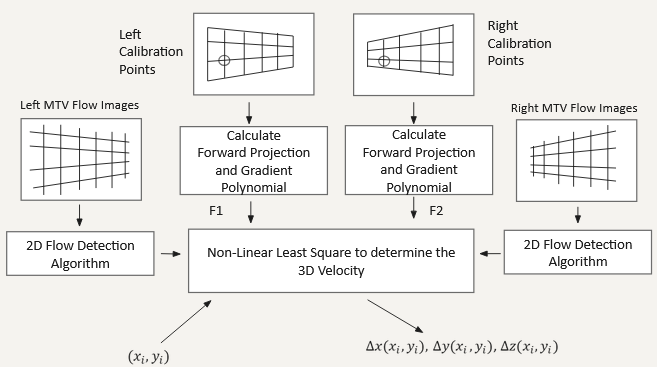
For the calibration process, the calibration object (checkerboard in this case) will be moves along positve and negative z coordinate at several coordinates. The object coordinate of the feature points are noted and the image plane coordinate of the two projected checkerboard are determined using corner detection methods. Using nonlinear least square methods, the transformation coefficients in the Soloff polynomial are obtained. From the velocity schematic, the gradient of the Soloff polynomial is determined and used to resolve the 3D velocity field with two set of 2D velocity fields.

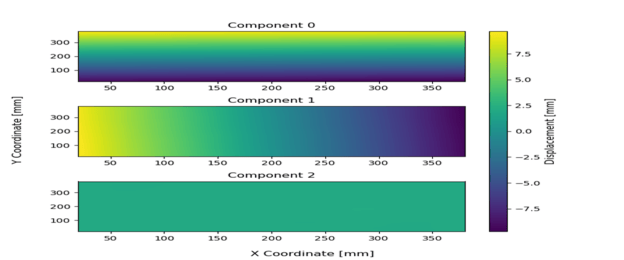
3D Velocity Field Reconstruction

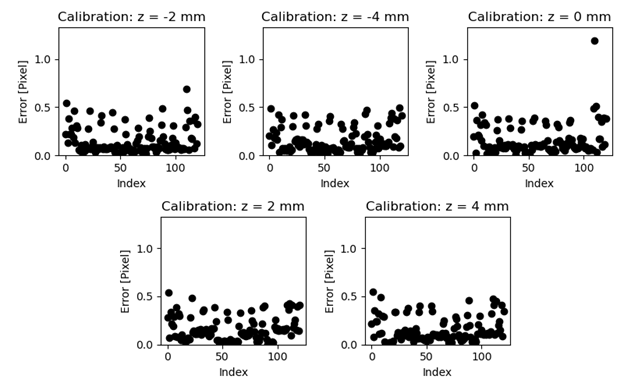
On the left, the projection error of the object onto the image plane. On the right, the root mean square error of object to image plane projection.

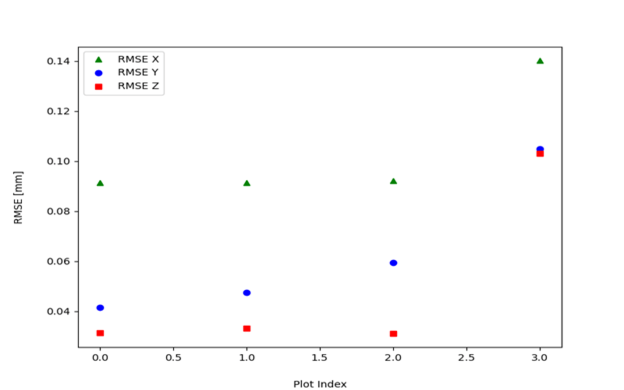
Evaluation

The forward projection of the object to image plane shows great agreement between across all calibration samples which is to be expected. The root mean square error of the projection falls under 0.1 for x and y projection and 0.14 for the z projection. Since there are less sample points in the z axis, it is reasonable for the error to be greater than the x and y axis.

The rotational velocity field from the two cameras of the stereoscopic setup.

On the left, the 3D displacement is resoved using the Soloff polynomial. On the right, the relative error of the 3D displacement is resolved.

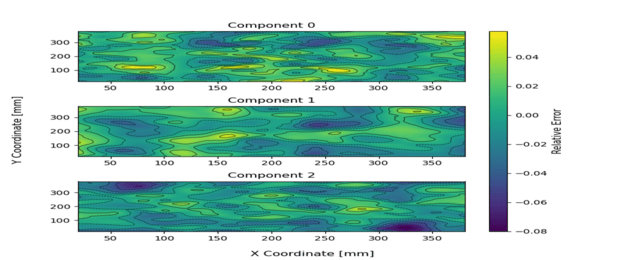
From the experimental result, Soloff polynomial based 3D reconstruction have a range of error bounded by (-0.08, 0.06). From further experimentation, it is concluded that the method described in the post provide a sufficiently accurate method to extract 3D velocity information from two sets of 2D velocity information. The method assumes: 1. the provided 2D velocity information is accurate and 2.there exist no alignment issues during the calibration process due to the inperfection in alignment with the actual laser sheet. One possible method to avoid the misalignment issues is to use the laser sheet itself as the calibration target.

Conclusion

Molecular Tagging Velocimetry combined with stereoscopic techniques offers a robust and accurate approach for measuring 3D velocity fields in high-speed flows. The use of the Soloff polynomial for geometric calibration ensures precise mapping between object and image planes, enabling reliable velocity reconstruction. The evaluation of projection errors and root mean square errors demonstrates that the method achieves high accuracy, with bounded error ranges for 3D displacement. While the approach relies on accurate 2D velocity data and careful alignment during calibration, incorporating the laser sheet as a calibration target could further mitigate alignment challenges. This study underscores the potential of stereoscopic MTV as a valuable tool for advanced flow diagnostics, particularly in extreme flow conditions.

References

[1] Bohl, D. G., Koochesfahani, M. M., & Olson, B. J. (2001). Development of stereoscopic molecular tagging velocimetry. Experiments in Fluids, 30(3), 302–308.

[2] Pavlík, D., Procházka, P., & Kopecký, V. (2016). Reconstruction of three-dimensional velocity vector maps from two-dimensional PIV data. Journal of Physics: Conference Series, 760, 012020. https://doi.org/10.1088/1742-6596/760/1/012020

[3] Ramsey, M. C., & Pitz, R. W. (2011). Template matching for improved accuracy in molecular tagging velocimetry. Experiments in Fluids, 51, 811–819. https://doi.org/10.1007/s00348-011-1098-y